🦌 ReHLine

ReHLine is designed to be a computationally efficient and practically useful software package for large-scale ERMs.

GitHub repo: https://github.com/softmin/ReHLine-python
Documentation: https://rehline.readthedocs.io
PyPi: https://pypi.org/project/rehline
Open Source: MIT license
Paper: NeurIPS | 2023

ReHLine is designed to be a computationally efficient and practically useful software package for large-scale ERMs.

The proposed ReHLine solver has four appealing linear properties:

It applies to any convex piecewise linear-quadratic loss function, including the hinge loss, the check loss, the Huber loss, etc.
In addition, it supports linear equality and inequality constraints on the parameter vector.
The optimization algorithm has a provable linear convergence rate.
The per-iteration computational complexity is linear in the sample size.

🔨 Installation

Install rehline using pip

pip install rehline

See more details in installation.

📮 Formulation

ReHLine is designed to address the empirical regularized ReLU-ReHU minimization problem, named ReHLine optimization, of the following form:

\[\min_{\mathbf{\beta} \in \mathbb{R}^d} \sum_{i=1}^n \sum_{l=1}^L \text{ReLU}( u_{li} \mathbf{x}_i^\intercal \mathbf{\beta} + v_{li}) + \sum_{i=1}^n \sum_{h=1}^H {\text{ReHU}}_{\tau_{hi}}( s_{hi} \mathbf{x}_i^\intercal \mathbf{\beta} + t_{hi}) + \frac{1}{2} \| \mathbf{\beta} \|_2^2, \ \text{ s.t. } \mathbf{A} \mathbf{\beta} + \mathbf{b} \geq \mathbf{0},\]

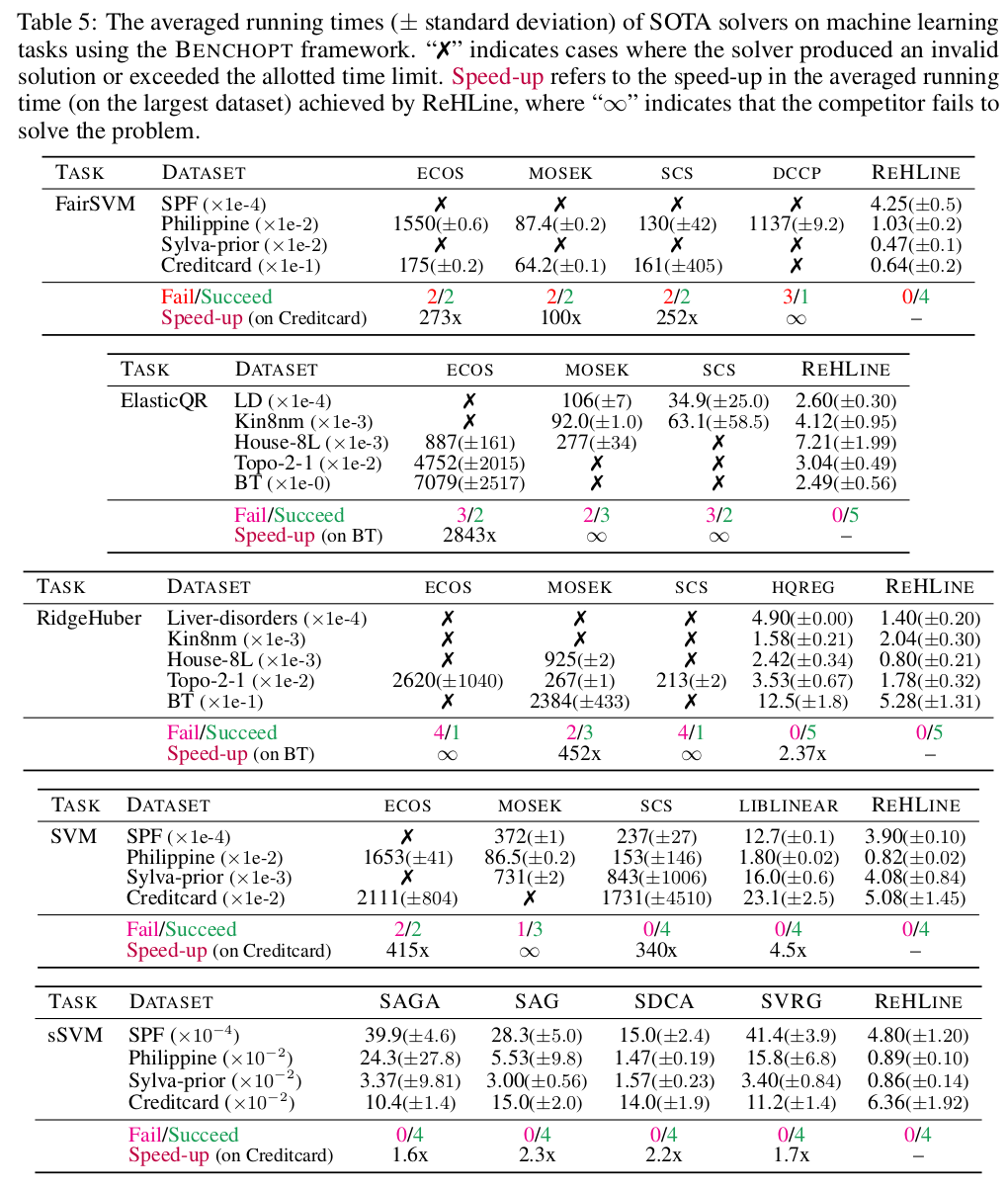
where \(\mathbf{U} = (u_{li}),\mathbf{V} = (v_{li}) \in \mathbb{R}^{L \times n}\) and \(\mathbf{S} = (s_{hi}),\mathbf{T} = (t_{hi}),\mathbf{\tau} = (\tau_{hi}) \in \mathbb{R}^{H \times n}\) are the ReLU-ReHU loss parameters, and \((\mathbf{A},\mathbf{b})\) are the constraint parameters. This formulation has a wide range of applications spanning various fields, including statistics, machine learning, computational biology, and social studies. Some popular examples include SVMs with fairness constraints (FairSVM), elastic net regularized quantile regression (ElasticQR), and ridge regularized Huber minimization (RidgeHuber).

📚 Benchmark (powered by benchopt)

To generate benchmark results in our paper, please check ReHLine-benchmark.

Problem	Results
FairSVM	Result
ElasticQR	Result
RidgeHuber	Result
SVM	Result
sSVM	Result

Note: You may select the “log-log scale” option in the left sidebar, as this will significantly improve the readability of the results.

🧾 Overview of Results

Reference

If you use this code please star the repository and cite the following paper:

@article{daiqiu2023rehline,
title={ReHLine: Regularized Composite ReLU-ReHU Loss Minimization with Linear Computation and Linear Convergence},
author={Dai, Ben and Yixuan Qiu},
journal={Advances in Neural Information Processing Systems},
year={2023},
}